Leetcode上面的一道题,原题传送门。
问题描述
给定一棵二叉树,让你判断,这棵二叉树是否关于根节点轴对称。
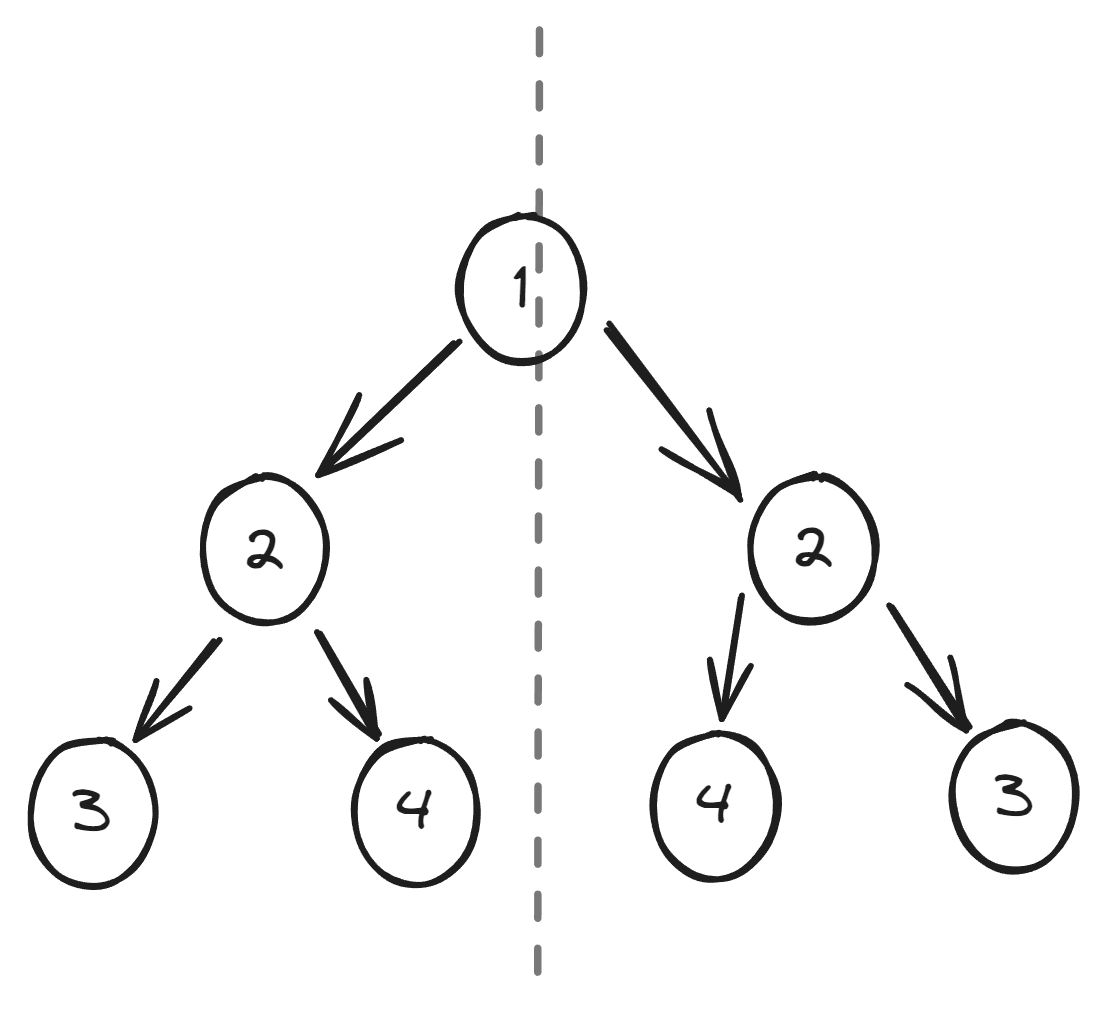
输入: root = [1,2,2,3,4,4,3]
输出: true
问题分析
这道题思路比较简单,二叉树可以通过中序+前序或者中序+后序确定,对于判断两棵树是否对称,也就是一棵树按照从左到右的顺序执行前序和中序生成的序列是会和另一个对称的树按照从右到左的顺序执行前序和中序生成的序列一样。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| #include <string>
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if (root == nullptr) {
return true;
}
if (root->left == nullptr && root->right == nullptr) {
return true;
}
std::string leftPreOrder = preOrder(root->left);
std::string rightPreOrder = preOrder(root->right, true);
if (leftPreOrder.compare(rightPreOrder) != 0) {
return false;
}
std::string leftInOrder = inOrder(root->left);
std::string rightInOrder = inOrder(root->right, true);
if (leftInOrder.compare(rightInOrder) != 0) {
return false;
}
return true;
}
std::string inOrder(TreeNode* root, bool isRTL = false) {
if (root == nullptr) {
return "o";
}
std::string order = "";
order = order.append(std::to_string(root->val));
TreeNode* next = isRTL ? root->right : root->left;
std::string left = inOrder(next, isRTL);
order = order.append(left);
next = isRTL ? root->left : root->right;
std::string right = inOrder(next, isRTL);
order = order.append(right);
return order;
}
std::string preOrder(TreeNode* root, bool isRTL = false) {
if (root == nullptr) {
return "o";
}
std::string order = "";
TreeNode *next = isRTL ? root->right : root->left;
std::string left = preOrder(next, isRTL);
order = order.append(left);
order = order.append(std::to_string(root->val));
next = isRTL ? root->left : root->right;
std::string right = preOrder(next, isRTL);
order = order.append(right);
return order;
}
};
|
按照这里的分析,对子树为空输出字符串做一下特别处理,避免误判。
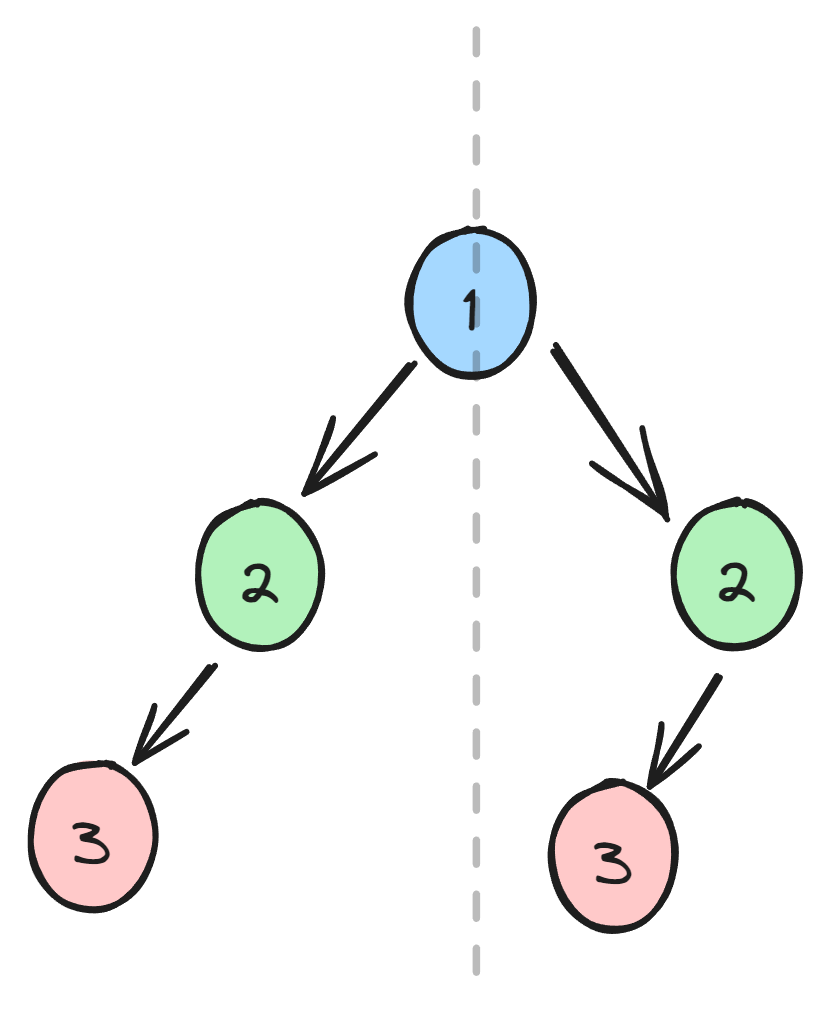
也就是上图👆这种情况
提交优化
提交后结果如下:
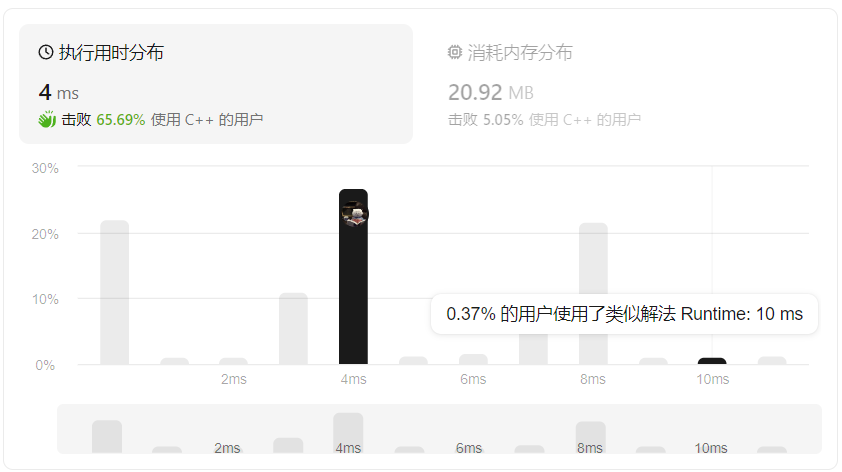
内存方面可以复用字符串,或者使用链表进行优化。这里对树遍历采用的是
递归的方式。使用非递归的方式可以减少内存的占用。



